MPGOS is designed to solve large number of independent and identical ODE systems using the massively parallel environment of GPUs
The strength of the package is demonstrated via few reference computations summarised below
Performance comparison with odeint (C++) and with DifferentialEquations.jl (Julia) of the low-dimensional Lorenz system:
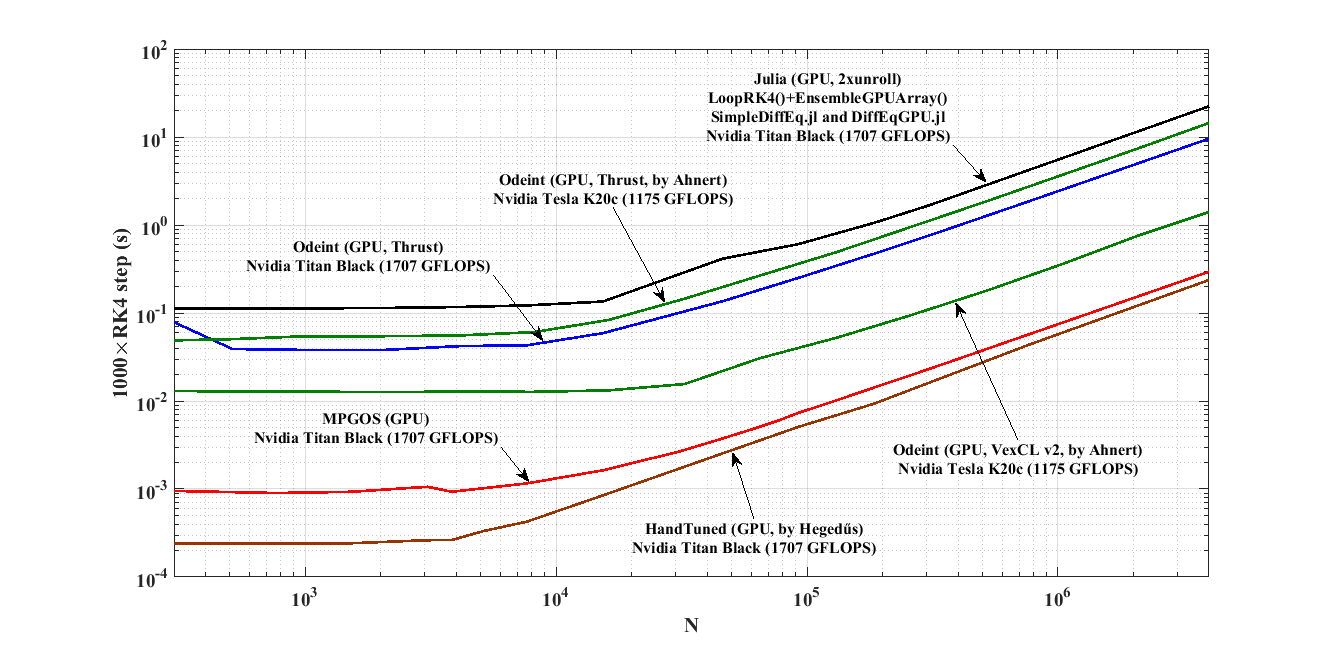
The solution of 1000, 4th order Runge-Kutta steps (fixed time steps) of the ensemble of N Lorenz system. The green data of ODEINT is taken from "Ahnert et al., (2014) Solving Ordinary Differential Equations on GPUs, in: Numerical Computations with GPUs pp. 125-157". The Julia code is implemented according to the tutorial example available in "https://github.com/JuliaDiffEq/DiffEqGPU.jl" (implemented by Dániel Nagy, n.nagyd@gmail.com).
Performance comparison with odeint (C++) and with DifferentialEquations.jl (Julia) of a system (Keller-Miksis equation) having large time scale differences:
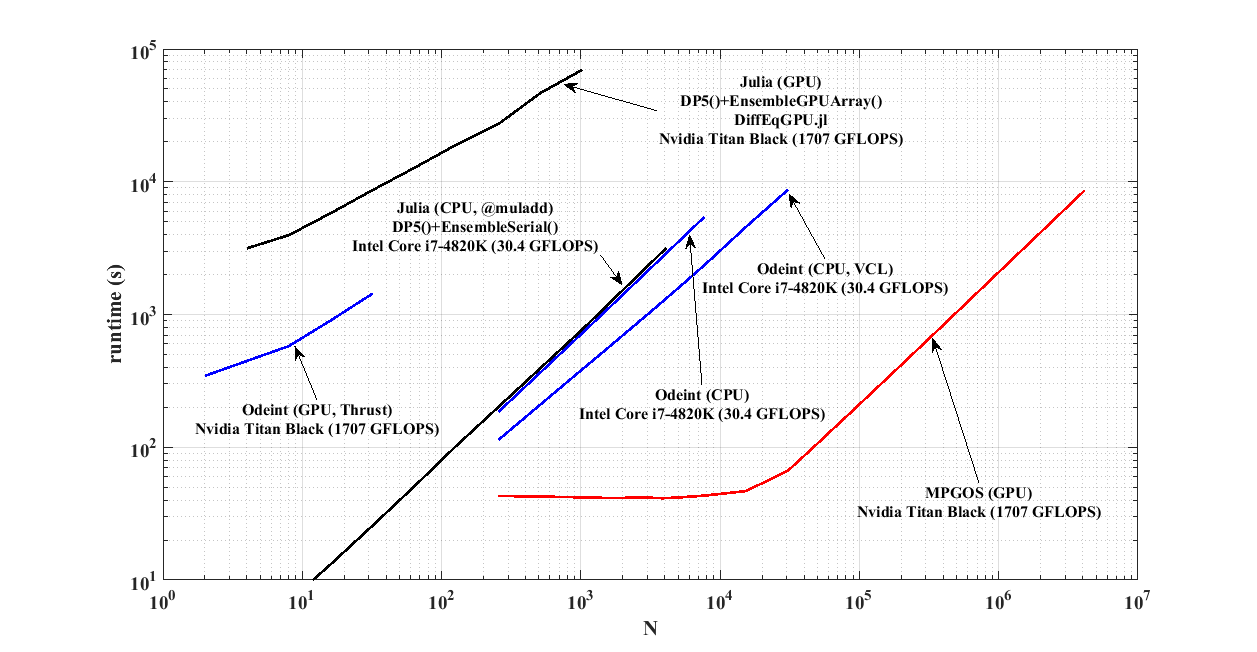
The solution of the ensemble of N Keller-Miksis equations. The solutions of each instance of the ODE system have large time scale differences. Therefore, the separation of the time co-ordinates of the independent instances is mandatory for good performance. The ODEINT versions are implemented by Lambert Plavecz (plaveczlambert@gmail.com), the DifferentialEquations.jl versions are implemented by Dániel Nagy, (n.nagyd@gmail.com). VCL means explicit vectorisation via Vector Class Library written by Agner Fog. For more details, the interested reader is referred to the Manual of MPGOS.
Performance comparison with odeint (C++) and with DifferentialEquations.jl (Julia) of a system exhibit impact dynamics:
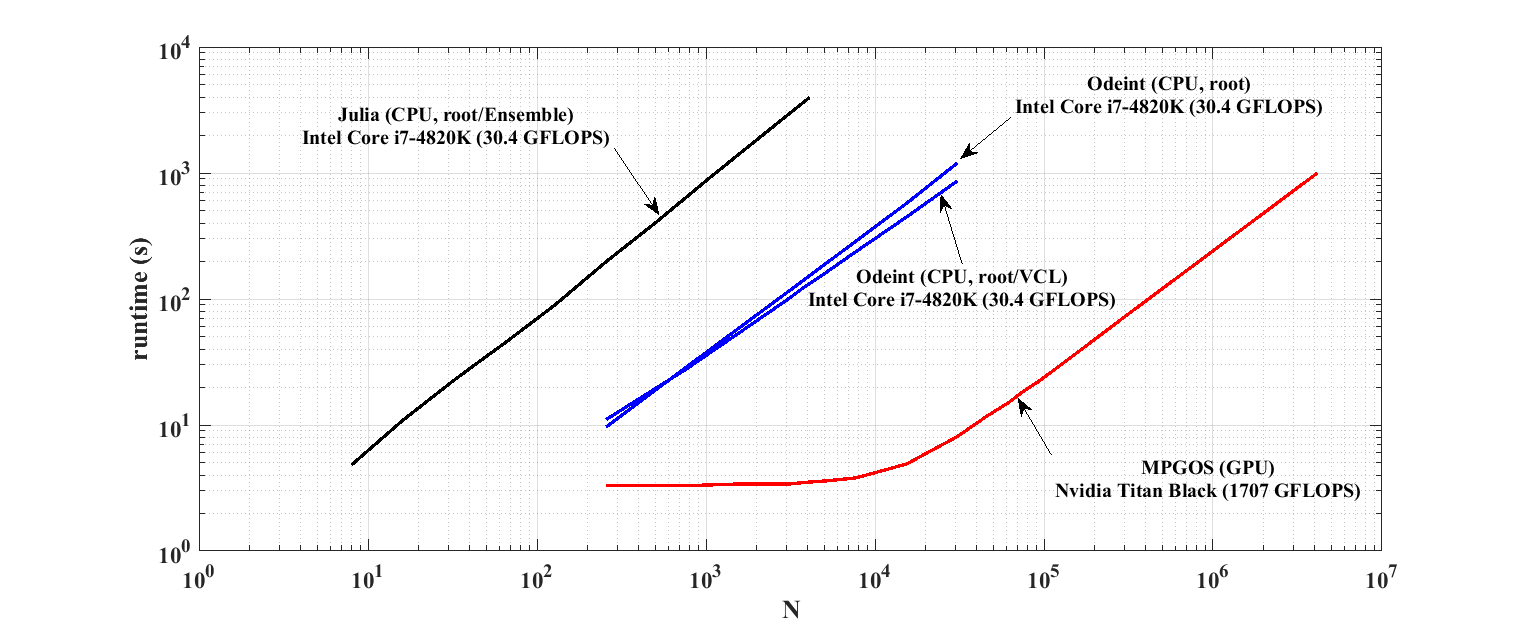
The solution of the ensemble of N system of pressure relief valve model. The solutions of each instance of the ODE system can exhibit impact dynamics. Therefore, the efficient handling of event detection and trajectory manipulation among a massive number of threads is mandatory for good performance. The odeint versions are implemented by Lambert Plavecz (plaveczlambert@gmail.com), the DifferentialEquations.jl versions are implemented by Dániel Nagy, (n.nagyd@gmail.com). Using GPUs, this special problem can be handled properly only by MPGOS. For more details, the interested reader is referred to the manual of MPGOS.
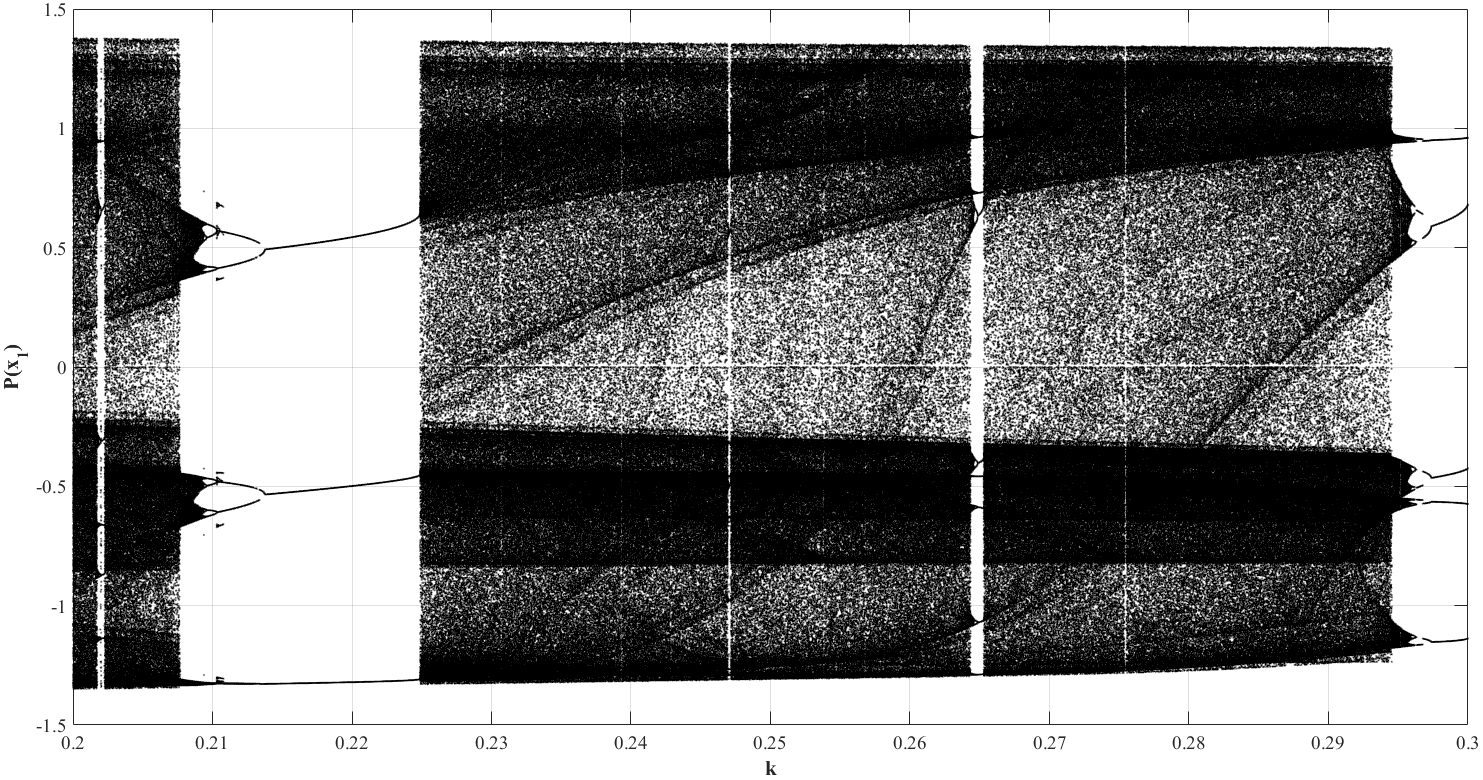
High-resolution (46 thousands) 1D bifurcation diagrams within 6 seconds (including the writing of data into disc):
The system is the nonlinear, second order, harmonically driven Duffing oscillator with 1024 transient iterations and 64 converged iterations to store the Poincaré sections (vertical axis). GPU: Nvidia GTX Titan Black (1707 GFLOPS double precision processing power)
6-dimensional parameter study - the scan of 2 billion parameter sets within 2 weeks:
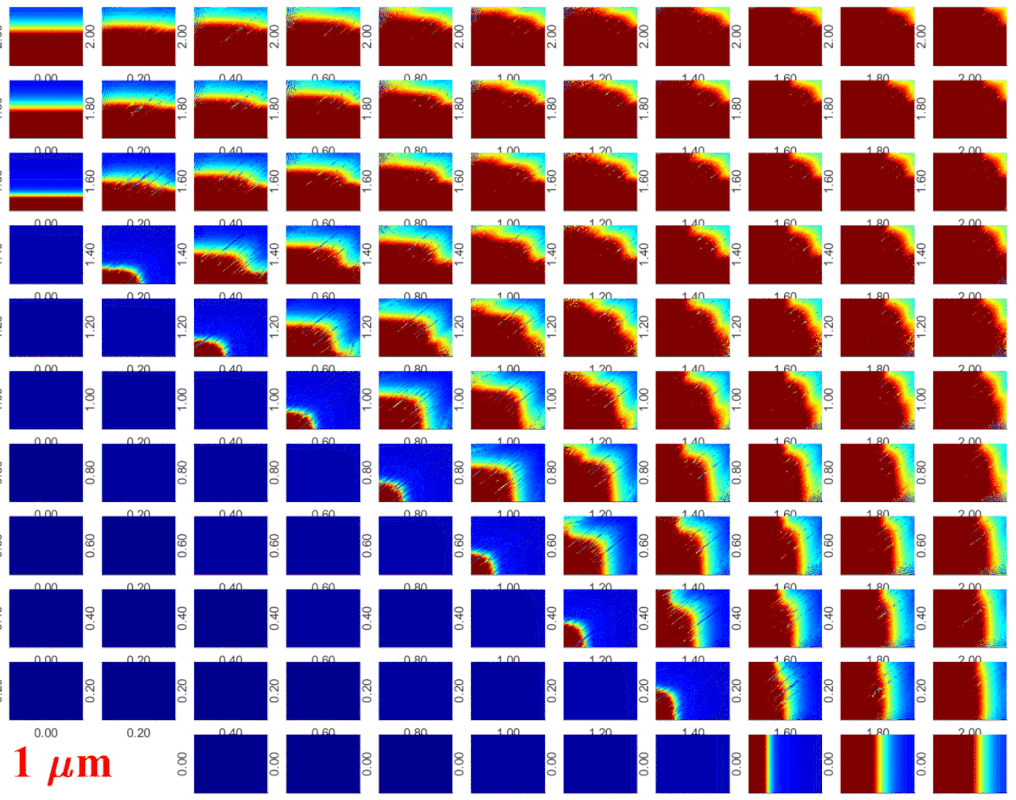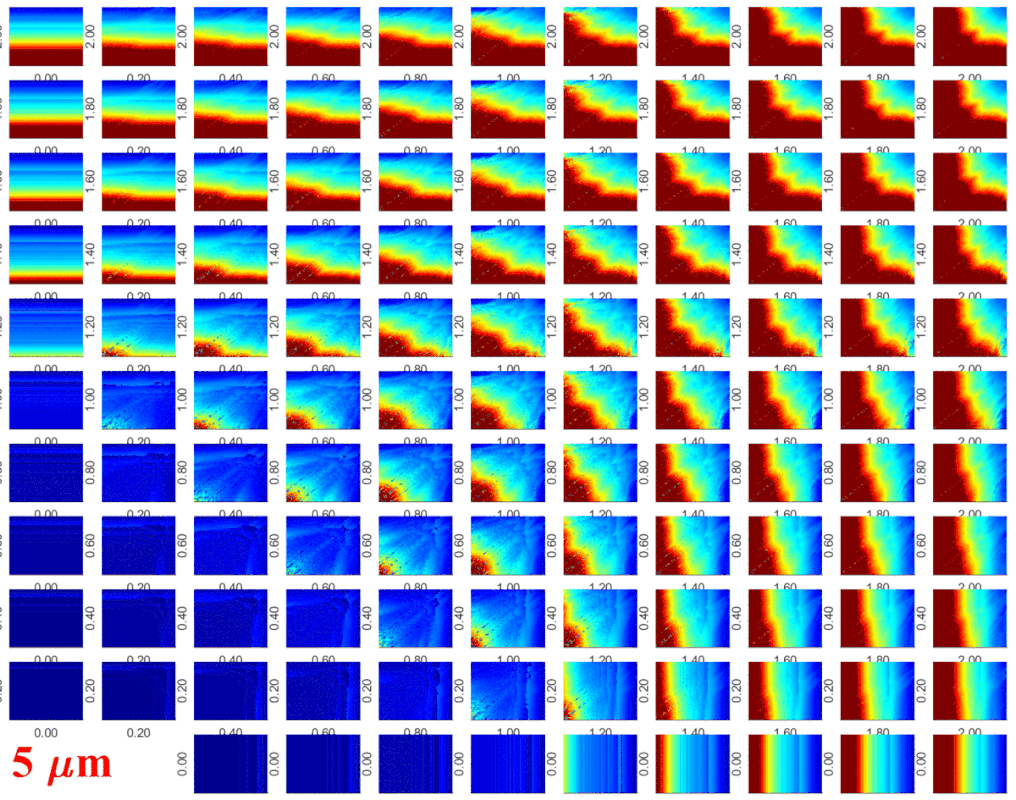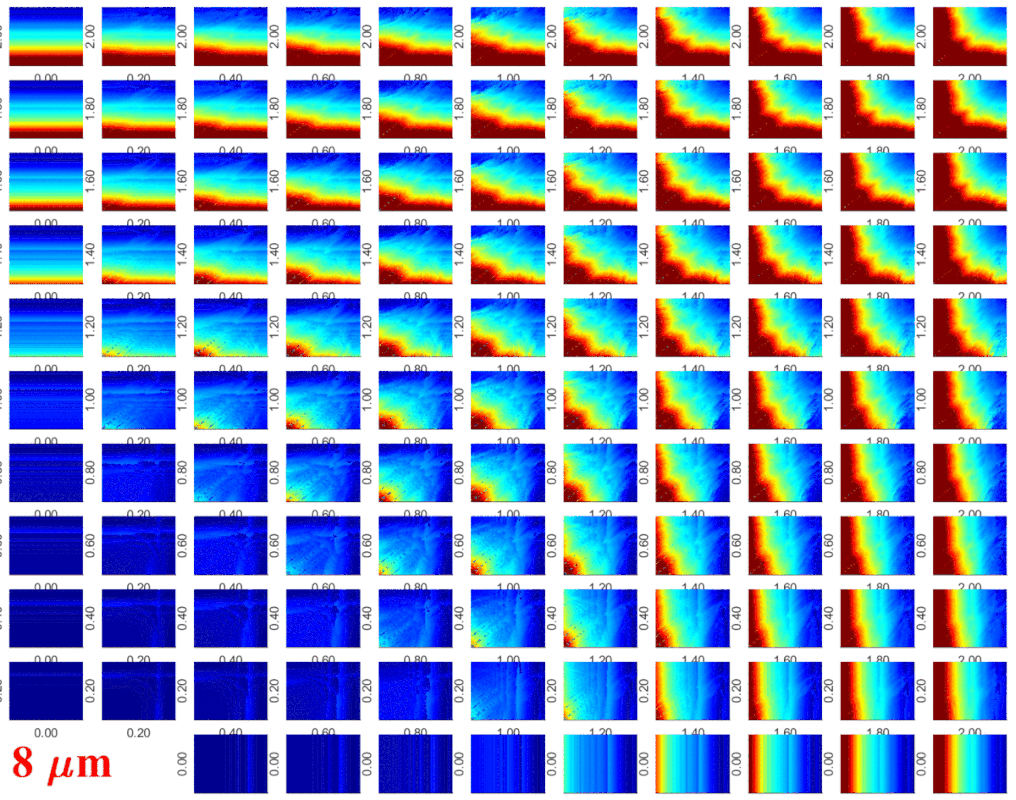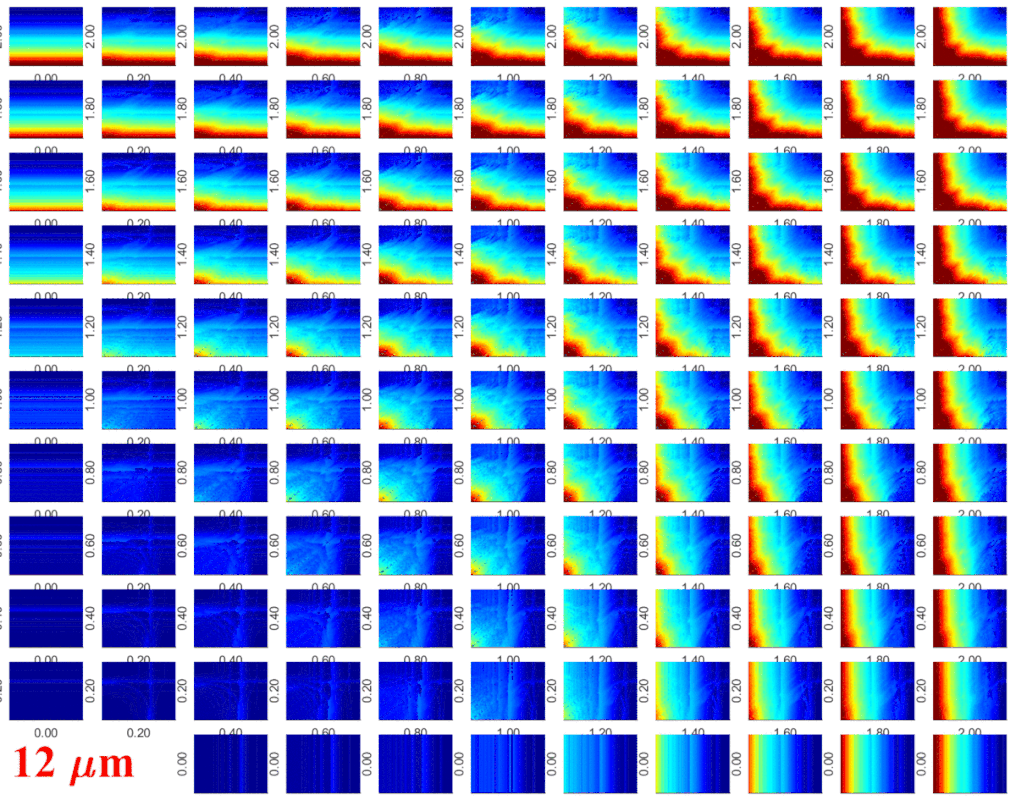
Dual-frequency driven Keller-Miksis equation (second order) describing the radial pulsation of a single bubble. The colour code is the collapse strength of the bubble that is an important measure for the scientific field of sonochemistry. The first 1024 collapses are regarded as initial transients, the next 64 collapse strengths are recorded. GPUs: 2xNvidia Tesla P100 (2x4.7 TFLOPS double precision processing power). In cooperation with the Drittes Physikalisches
Institut, Georg-August-Universität Göttingen, Göttingen (Prof. Dr. Werner Lauterborn and Dr. Robert Mettin); and with the Max Planck Institute
for Dynamics and Self-Organization, Göttingen, Germany (Prof. Dr. Ulrich Parlitz).
High-resolution (250 million) bi-parametric plots within 4 weeks:
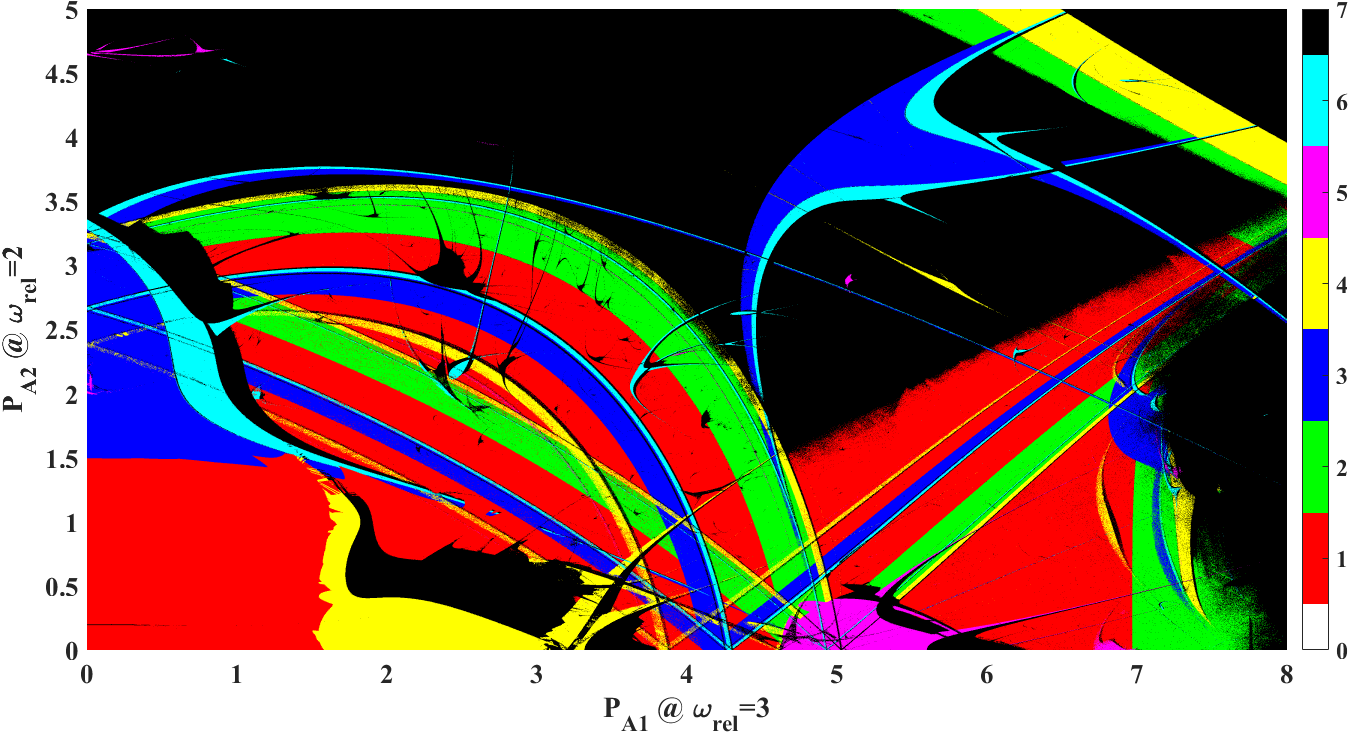
Dual-frequency driven Keller-Miksis equation (second order) extended with its linearised system in polar coordinates. Thus, altogether we have a 4 order ODE system. The equation describes the dynamics of a single spherical bubble. The number of the transient iterations is 1024 followed by 2048 iterations for the proper convergence of the Lyapunov exponents. In the picture, the period of the attractors found are plotted. GPUs: 1x Nvidia GTX Titan Black (1707 GFLOPS double precision processing power), 2x Nvidia Tesla K20 (1175 GFLOPS double precision processing power) and 8x Nvidia Tesla M2050 (515 GFLOPS double precision processing power). In cooperation with the Drittes Physikalisches
Institut, Georg-August-Universität Göttingen, Göttingen (Prof. Dr. Werner Lauterborn and Dr. Robert Mettin); and with the Max Planck Institute
for Dynamics and Self-Organization, Göttingen, Germany (Prof. Dr. Ulrich Parlitz).
Efficient handling of impact dynamics, grazing lines using 1 million initial conditions with simulation time 4s:
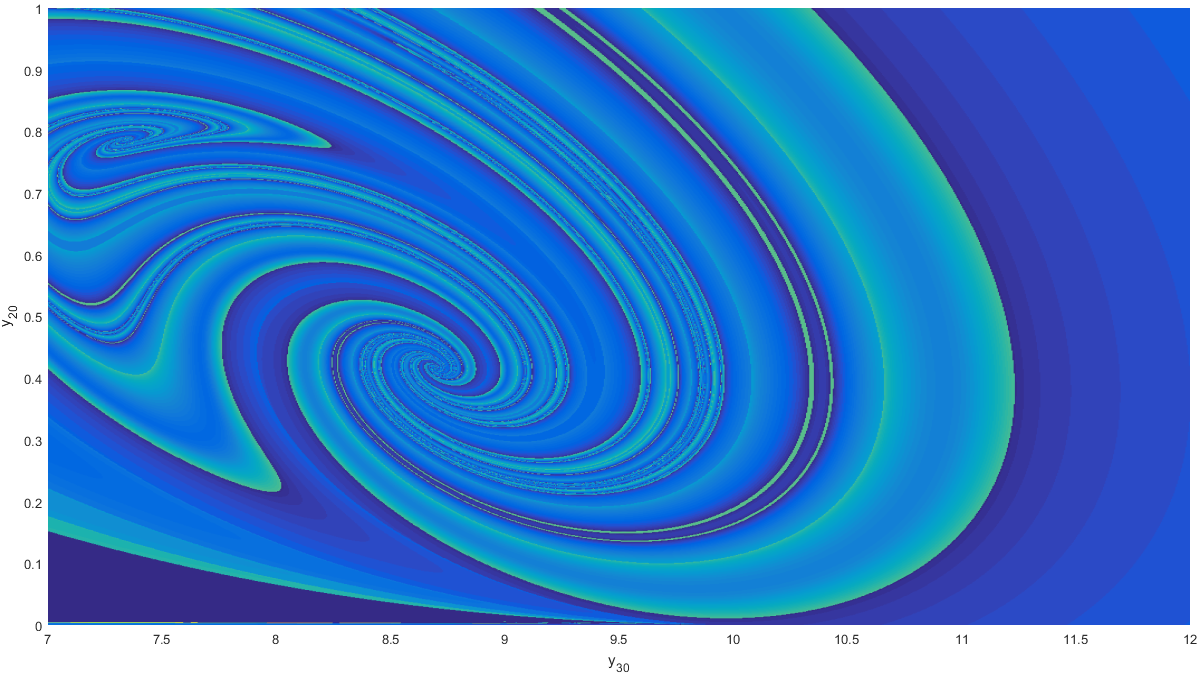
Grazing lines of a pressure relief valve (third order ODE) using 1024X1024 number of initial conditions. This problem demonstrates the efficient handling of impact dynamics. In cooperation with Dr. Csaba Hős from the Budapest University of the Technology and Economics, Department of Hydrodynamics Systems. GPU: Nvidia GTX Titan Black (1707 GFLOPS double precision processing power)